赛事评分算法介绍

评分算法使用 Wasserstein 距离(wasserstein metric)算得的 loss 函数作为评分结果。

背景知识介绍

KL 散度和 JS 散度经常被用来定义两个分布之间的距离，其定义如下：

KL 散度

KL 散度：

$$KL(p \| q) = \int_{\mathbb{R}^n} p(x) \log \frac{p(x)}{q(x)} \mathrm{d}x$$

KL 散度又称为相对熵(relative entropy)，与 fisher 信息矩阵有关，衡量的是用分布函数 $q(x)$ 来近似分布函数 $p(x)$，所损失的信息。

JS 散度

JS 散度(Jensen–Shannon divergence)：

$$JS(P_1 \| P_2) = \frac{1}{2} KL \left( P_1 \middle\| \frac{P_1+P_2}{2} \right) +\frac{1}{2} KL \left( P_2 \middle\| \frac{P_1+P_2}{2} \right)$$

JS 散度又称为信息半径(information radius)，在 KL 散度的基础上有所修正，解决了不对称的问题，并且更加平滑。

JS 散度是有界的(以 2 为底数的话值域为 $[0,1]$ )

Wasserstein 距离的数学定义

Wasserstein 距离(又叫 Earth-Mover 距离)是衡量两个分布之间距离的一个函数，数学定义如下：

$$W_p(\mu,\nu):= \inf_{\gamma \in \Gamma(\mu, \nu)} \left(\int_{\mathbb{R}^n \times \mathbb{R}^n}d(x,y)^p \; \mathrm{d}\gamma(x,y)\right)^{1/p} = \left(\inf_{\xi } \mathbb{E}[d(x,y)^p]\right)^{1/p}$$

Wasserstein 距离相比 KL 散度和 JS 散度的优势在于，即使两个分布的支撑集没有重叠或者重叠非常少，仍然能反映两个分布的远近。而 JS 散度在此情况下是常量，KL 散度可能无意义。

直观理解

Wasserstein 距离的直观解释：

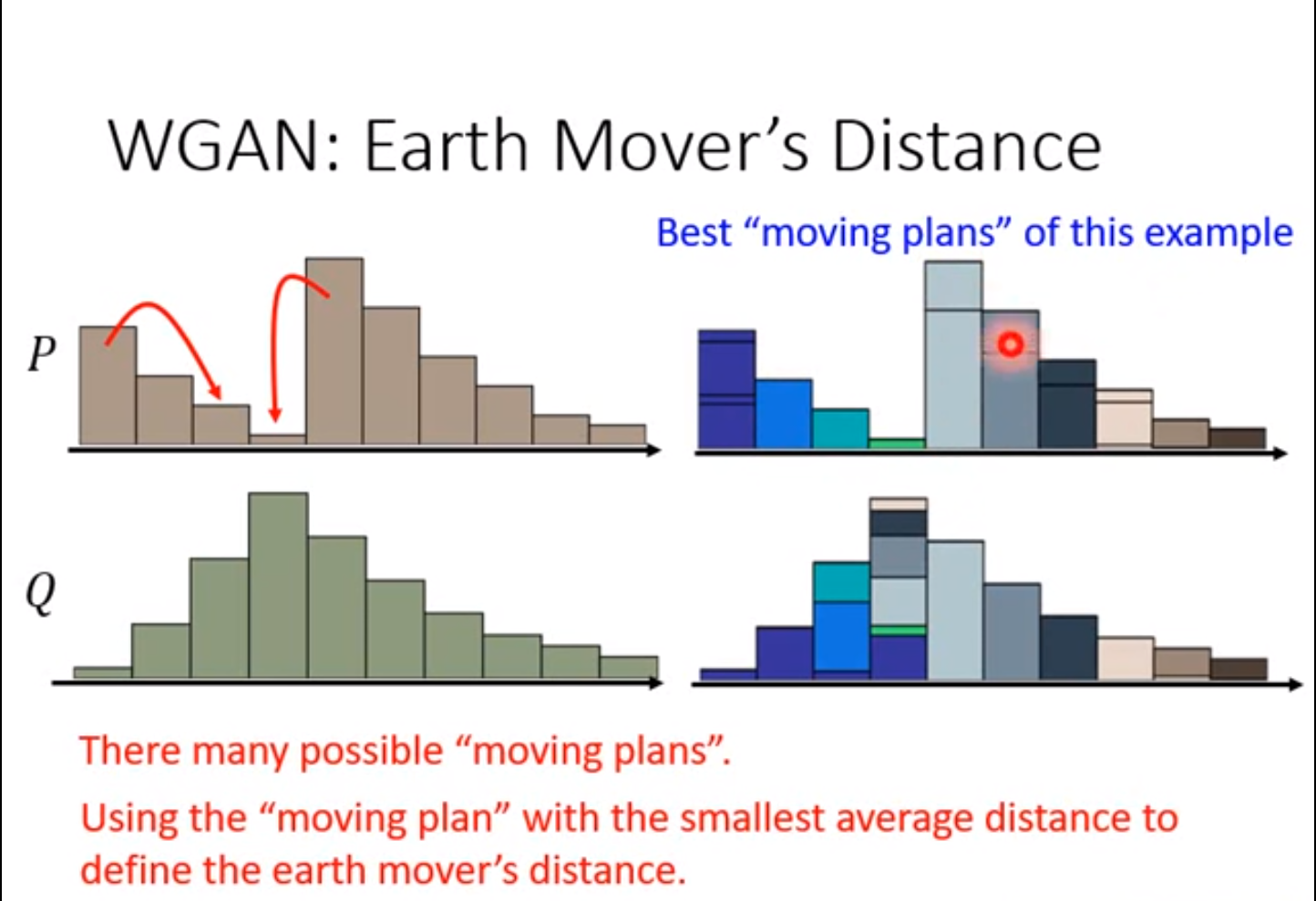
Wasserstein 距离实际上是最优传输问题(optimal transport)中的概念，指的是把概率分布 $q$ 转换为 $p$ 的最小传输质量(概率密度在离散情况下，叫做概率质量)，也叫做最优传输距离或者推土机距离。

比赛中使用的评分算法

比赛中给出的数据为计算机模拟的 PMT 波形数据，参赛者要求从这些波形数据中找出中微子信号出现的时间戳。

我们用参赛者提交的时间戳(看作一个离散分布)，与真实的事件发生时间(看作一个离散分布)之间的 Wasserstein 距离作为评分标准。